本文将从矩阵的本质、矩阵的原理、矩阵的应用三个方面，带您一文搞懂人工智能数学基础-线性代数之矩阵。

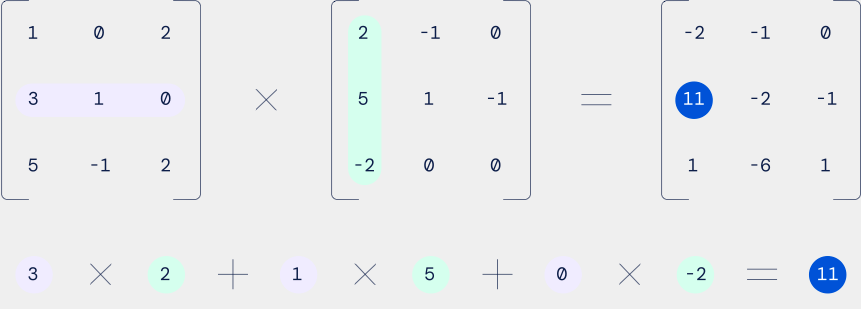
一、矩阵的本质

点积（Dot Product）：点积作为向量间的一种基本运算，通过对应元素相乘后求和来刻画两向量的相似度和方向关系。

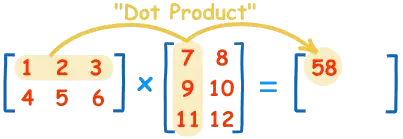点积（Dot Product）

一、定义

点积，又称为数量积或标量积，是两个同维度向量之间的一种运算。对于两个n维向量A和B，点积是将它们的对应元素相乘后求和得到的结果。

二、符号表示

点积通常使用符号"·"或"<A, B>"来表示。即，若A和B是两个向量，则它们的点积可以表示为A·B或<A, B>。

三、计算方法

1. 确保向量A和B的维度相同，即它们都有n个元素。
2. 将向量A和B的对应元素相乘，得到n个乘积。
3. 将这n个乘积相加，得到最终的点积结果。

数学公式表示为：A·B = a1b1 + a2b2 + ... + an*bn，其中ai和bi分别是向量A和B的第i个元素。

矩阵（Matrix）：矩阵是数值的矩形阵列，通过特定的运算规则（如矩阵乘法），在数学、科学及工程领域中实现数据变换和问题解决的关键工具。

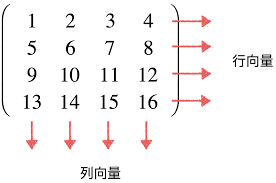矩阵（Matrix）

一、定义

矩阵是一个数值的矩形阵列，它在数学、物理学、工程学和计算机科学等多个领域中都有广泛应用。矩阵由行和列组成，每个元素在矩阵中都有确定的位置。

二、符号表示

矩阵通常用大写的粗体字母表示，例如A、B、C等。矩阵的尺寸由其行数和列数决定，一个m×n的矩阵表示它有m行和n列。

矩阵中的每个数值被称为元素。元素的位置由其所在的行和列决定，通常用下标表示。例如，在矩阵A中，第i行第j列的元素可以表示为A[i][j]。

三、矩阵乘法

矩阵乘法是一种特殊的运算，不同于常规的元素间乘法。对于两个矩阵A和B，只有当A的列数等于B的行数时，它们才能进行矩阵乘法。结果矩阵C的尺寸是A的行数乘以B的列数。

矩阵乘法的计算遵循以下步骤：

1. 验证矩阵A的列数是否等于矩阵B的行数。如果不相等，则无法进行矩阵乘法。
2. 创建一个新的矩阵C，其行数与矩阵A相同，列数与矩阵B相同。
3. 对于矩阵C中的每个元素C[i][j]，计算它是矩阵A的第i行与矩阵B的第j列的对应元素乘积之和。即，C[i][j] = A[i][k1] * B[k1][j] + A[i][k2] * B[k2][j] + ... + A[i][kn] * B[kn][j]，其中k1, k2, ..., kn是矩阵A的列索引或矩阵B的行索引。   

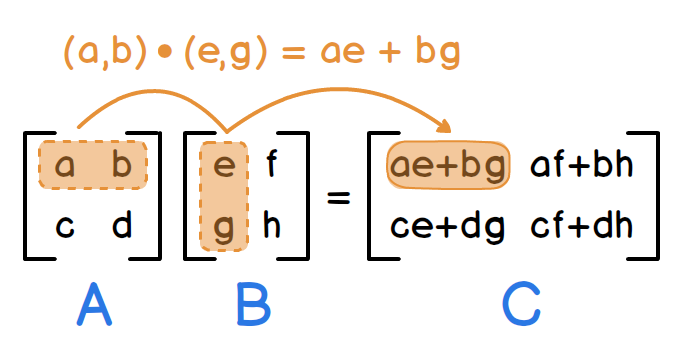矩阵乘法

二、矩阵的原理

线性方程组求解：将N元一次方程组转化为矩阵运算，可以简化求解过程，提高计算效率，并在多个领域中得到广泛应用。

齐次线性方程组

一、线性方程组的基本概念

1. 定义：线性方程组是由一组线性方程（即未知数的次数均为1的方程）构成的集合。每个方程可以表示为ax + by + ... + z = c的形式，其中a, b, ...是常数，x, y, ..., z是未知数。
2. 表示：线性方程组通常可以用矩阵形式来表示。具体地，我们可以将方程组的系数提取出来形成一个系数矩阵，将常数项组成一个常数向量，从而将原方程组转化为矩阵方程。

二、线性方程组的矩阵表示

1. 系数矩阵：对于线性方程组中的每个方程，将其未知数前的系数提取出来，按照方程的顺序排列成一个矩阵，称为系数矩阵（记为A）。
2. 常数向量：将线性方程组中的常数项（即等号右边的数值）按照方程的顺序排列成一个列向量，称为常数向量（记为b）。
3. 未知数向量：定义一个列向量，其元素个数与线性方程组中的未知数个数相同，用于表示未知数的解，称为未知数向量（记为x）。
4. 矩阵方程：将系数矩阵、常数向量和未知数向量结合起来，形成矩阵方程Ax = b，其中A是系数矩阵，x是未知数向量，b是常数向量。

三、线性方程组的求解方法

1. 高斯消元法：

• 通过一系列行变换（交换行、倍加行、倍减行），将系数矩阵变换为上三角矩阵或对角矩阵。
• 从最后一行开始，逐步回代求解未知数。

2. 矩阵的逆：

• 如果系数矩阵A是可逆的（即存在逆矩阵A^(-1)），则可以通过计算逆矩阵直接求解未知数向量，即x = A^(-1)b。
• 注意：不是所有矩阵都有逆矩阵，只有满秩矩阵（行列式不为0）才可逆。

3. 克拉默法则：

• 利用行列式的性质，通过计算系数矩阵的行列式和伴随矩阵来求解线性方程组。
• 克拉默法则适用于任何规模的线性方程组，但计算量随着未知数个数的增加而急剧增加。

主成分分析（PCA）：主成分分析（PCA）是一种统计方法，用于简化数据集并揭示其内在结构。

主成分分析（PCA）

1.标准化数据集

在开始PCA之前，通常会对原始数据集进行标准化处理。标准化后的数据集将具有零均值和单位方差，这对于后续的计算和分析是重要的。

输出：标准化后的数据集矩阵。

2. 协方差矩阵

标准化数据集之后，计算其协方差矩阵。协方差矩阵捕获了数据集中各特征之间的关系和变化的幅度。

输出：协方差矩阵。

3. 特征值和特征向量

通过对协方差矩阵进行特征值分解，PCA得到一组特征值和对应的特征向量。特征值的大小反映了对应特征向量方向上数据变化的重要性。

输出：

• 特征值列表（按降序排列）。
• 对应的特征向量矩阵，其中每一列是一个特征向量。

4. 主成分

根据特征值的大小，选择前k个最大的特征值对应的特征向量作为主成分。这些主成分构成了一个新的低维空间，用于表示原始数据。

输出：主成分矩阵，其中每一列是一个主成分（即选定的特征向量）。

5. 投影数据

将原始数据投影到主成分构成的低维空间上，得到降维后的数据表示。

输出：投影后的数据集矩阵，其维度低于原始数据集。

三、矩阵的应用

马尔可夫矩阵：马尔可夫矩阵描述了系统中状态之间的转移概率，是马尔可夫链模型的核心，广泛应用于预测、决策、模式识别和强化学习等领域。

def print_markov_matrix(matrix, state_labels):  
    """  
    结构化输出马尔可夫矩阵，并附带状态标签。


    :param matrix: 马尔可夫矩阵  
    :param state_labels: 状态标签列表  
    """  
    num_states = len(matrix)  
    print(f"马尔可夫状态转移矩阵（{num_states}个状态）:")  
    print("    " + "   ".join(state_labels))  # 打印状态标签头部  
    for i in range(num_states):  
        row_data = [f"{matrix[i][j]:.2f}" for j in range(num_states)]  
        print(f"{state_labels[i]}: {'   '.join(row_data)}")  
  
# 示例：天气预测模型的状态转移矩阵  
states = ['晴天', '多云', '雨天']  
transition_matrix = [  
    [0.8, 0.15, 0.05],  # 晴天转移到其他天气的概率  
    [0.2, 0.7, 0.1],    # 多云转移到其他天气的概率  
    [0.1, 0.3, 0.6]     # 雨天转移到其他天气的概率  
]  
  
print_markov_matrix(transition_matrix, states)